In the previous part we made look through the distribution of sample means for three distributions: Uniform, Cauchy, and Petersburg distribution. The Cauchy and Petersburg distributions do not fulfill the Central Limit Theorem since they have infinite variance (and infinite expected value in “Petersburg” case). Now we will have a look at the numerical results for standard deviation of sample means. As in previous part, we use Uniform distribution only as a reference since it fulfills CLT and we use the same pseud-random number generator (Mersenne-Twister).

Uniform distribution, gives a really nice impressions when looking through the chart showing standard deviation \(\sigma\) vs sample size \(n\):

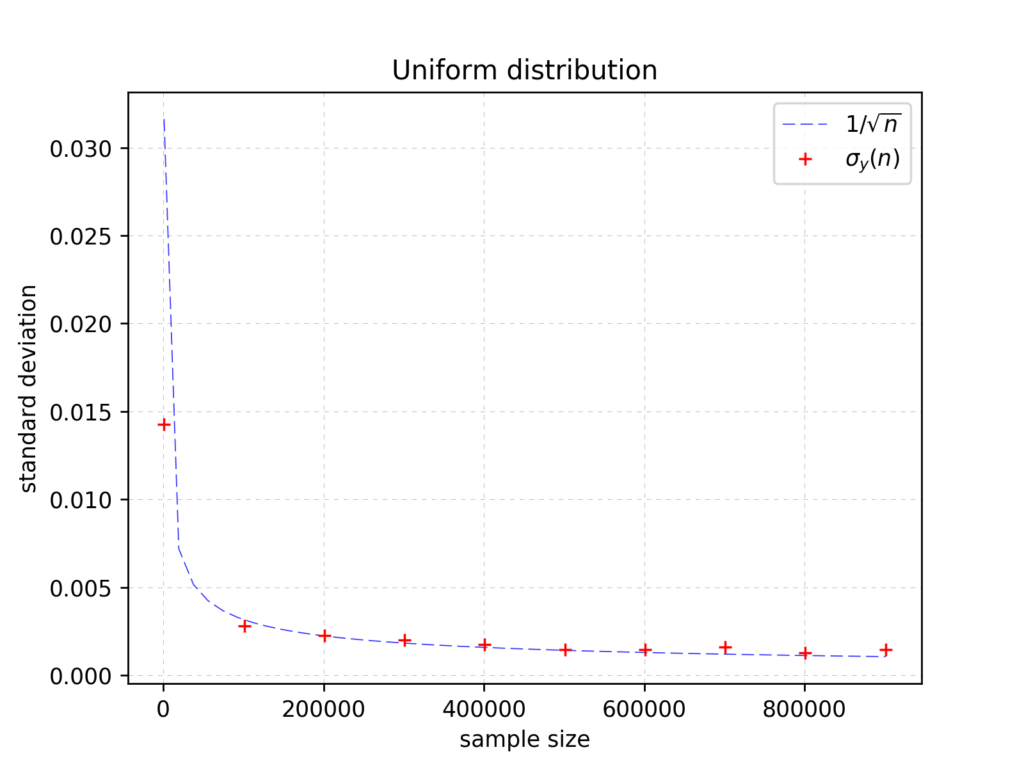
It behaves as we expected – in accordance to the CLT – it varies like: \(\frac{1}{\sqrt{n}}\).

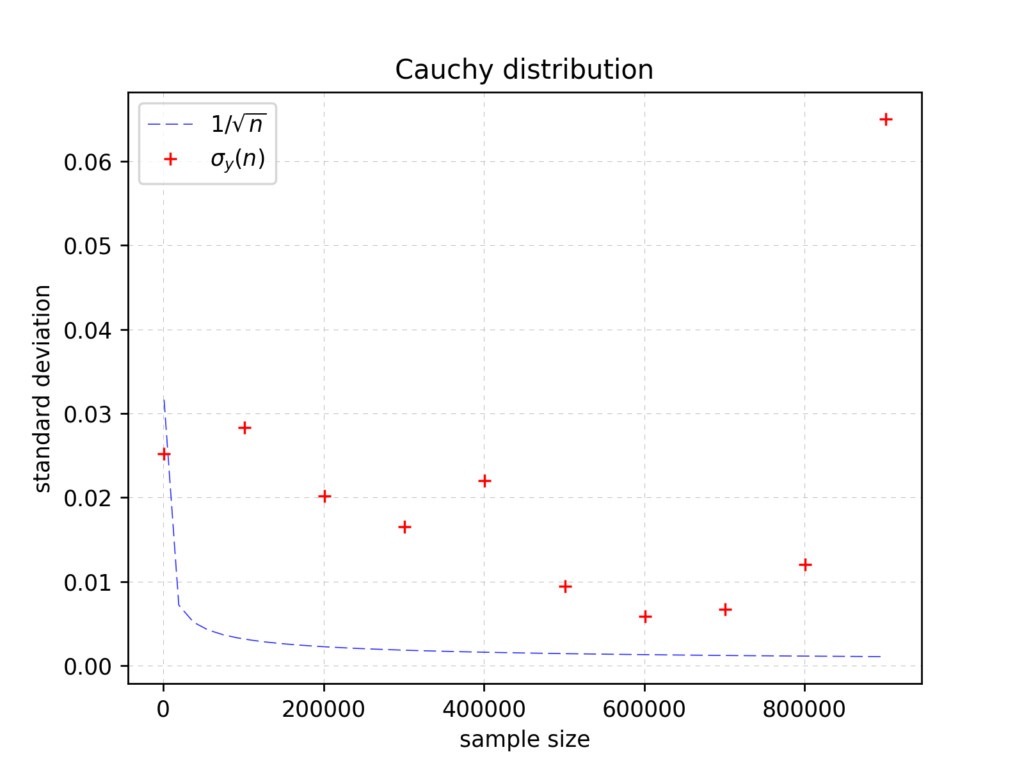
And now – stars of our show – Cauchy distribution:

…and Petersburg distribution:

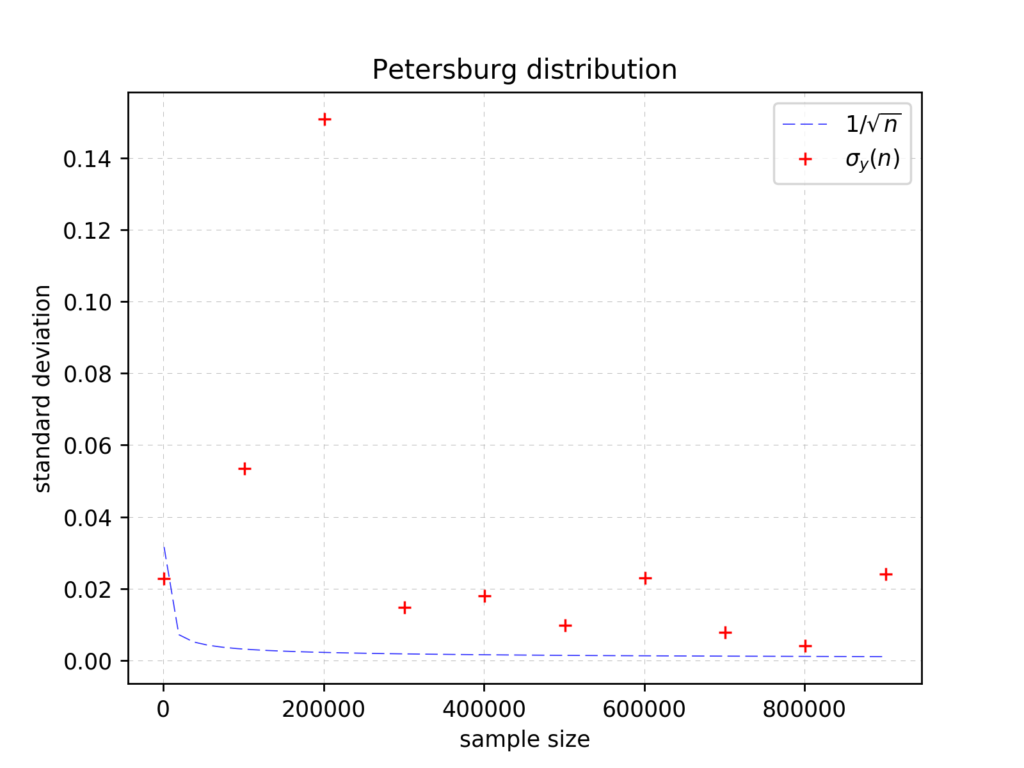
In spite of trying many different pseudo-random generator seed values the result is the roughly the same – \(\sigma(n)\) does not seem to converge.

Conclusions:

Since distributions of sample means for the Cauchy and Petersburg distributions do not fulfill the assumptions of CLT – we didn’t expected the same result as in “properly behaving distributions” like uniform distribution. In spite we didn’t discover anything new with our “experimental statistics”, we he had a lot of fun and wanted to share it with you.

Mikołaj Sitarz, 2018